cirkel en Π
Waarom zijn exacte vakken toch zo moeilijk?
Moet je mij niet vragen, want ik ben er
helemaal niet van overtuigd dat dat waar is.
Volgens mij zijn de exacte vakken een
didactisch achtegebleven (zo niet achtelijk) gebied. Wij exactelingen kunnen
namelijk nog altijd de schijn ophouden dat het de moeilijkheid van het vak is
die voor de matige resultaten zorgt. En het domme volk gelooft ons, haha. Toch
is het tijd voor een kultuuromslag, exactelingen moeten ook maar eens nadenken
over de didaktiek van het vak. Exacte vakken zijn maakbaar!
Een voorbeeld:
Het getal Π is voor alle schattingen te stellen op 3 daar moet je niet moeilijk over doen (de fout is dan maar 5% en dus te verwaarlozen)
De omtrek van een rond perk met bloemen is dan 3 x de doorsnede, je kan dus vrij eenvoudig afschatten hoeveel prikkeldraad je nodig hebt.
Als je dat aan het doen bent gebruik je ongemerkt 2Πr maar daar moet je niet vanuit gaan.
Hoeveel bollen je moet kopen hangt af van
de oppervlakte
Die kun je ook eenvoudig schatten de
oppervlakte van een cirkel is namelijk even groot als 3 vierkanten met een
zijde evengroot als de straal van de cirkel.
Even een tekeningetje:
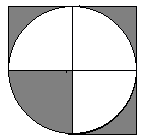
De grijze stukjes buiten de cirkel zijn
even groot als het grijze stukje in de cirkel (wat nou Πr2) Die r2 ‘zegt’ een vierkant met een zijde r en dat keer 3 simpel en
doeltreffend nietwaar?
De andere formule voor de oppervlakte van een cirkel is Π/4*D2
Wat zoveel betekent als 3/4 van de oppervlakte van een vierkant dat om de cirkel past en dus een zijde heeft van D (diameter)
Moet ik nog even doorgaan?
OK een hele moeilijke dan; de inhoud van
een mestopslag
we meten de omtrek door gewoon eromheen te
lopen met grote stappen (50 stappen, 50 meter), delen dat door 3 dan hebben we de
doorsnee (krap 17 meter)
De straal is dan ongeveer 8 meter
de oppervlakte van de bodem ( 3*64=192
vierkante meter) maal de mest hoogte (3 meter) levert een geschat volume van 576 kubieke meter
Hadden we dit uitgerekend met de precieze
formules en goed meten waren we aan de 3*Π(50/2Π)2 597 m3 een
afwijking van minder dan 1 %
Door uit te gaan van het natte vingerwerk kunnen we naar de formules en andere ellende toewerken en niet andersom.
Ik weet de diameter:
Ik weet de straal:
Ik weet de omtrek:
Ik weet de oppervlakte:
Ik weet de hoogte en de diameter (anders eerst even het cirkel gereedschapje gebruiken)
Ik weet de hoogte en de diameter (anders eerst even het cirkel gereedschapje gebruiken)
Ik weet de omtrek: diameter, oppervlakte, inhoud
Ik weet de diameter: omtrek oppervlakte, inhoud
Graden en radialen
Bij graden denk je vanuit het midden, bij radialen vanuit de omtrek
Radialen als hoekmaat.
Er zijn veel gelijkwaardige manieren om een hoek aan te geven, we zijn gewend aan graden waarbij een cirkel 360 graden (deg) beslaat.
Je zou een hoek ook in uren kunnen verdelen zodat een cirkel uit 12 uren bestaat. (gevaar op 9 uur)
Of een tandwiel met 40 tanden heeft een omtrek van 40 tanden en die kun je dus ook als hoekmaat gebruiken.
Cirkels hebben een omtrek die ook een hele cirkel is, de omtrek van een cirkel is 2Πr dus 2Π is ook een goede maat voor een hele cirkel.
Deze laatste hoekmaat wordt bijvoorbeeld door Excel gebruikt.
Ook rekenmachines hebben de mogelijkheid om ermee te werken.
Als een hoek wordt uitgedrukt in stukjes van de cirkelomtrek noemen we dit radialen (rad)
1 rad is dus gelijk aan 360/2Π = 57.296 graden
1 graad is dus 2Π/360 = 0.017 radialen
Rekenmachine in de DEG (degree = graden) modus
Rekenmachine in de RAD (radialen) modus
Van hoek naar sinus gebruik de sin functie van de rekenmachine
Van sinus naar hoek gebruik de sin-1 functie van de rekenmachine (shift sin)
even een weetje, de rekenmachine kent ook gra of grad, maar dat werkt met een cirkel van 400 graden die in dat geval gon genoemd wordt. Deze hoekmaat wordt in de geodesie en landmeterij wel gebruikt, een rechte hoek is dan 100 gon.
Ik weet de hoek in graden:
Ik weet de hoek in radialen:









